一.张弦桁架结构原理
张弦桁架结构是张弦梁结构的一种类型,其定义是,用撑杆连接上部抗弯受压构件和下部受拉构件(索)而形成的自平衡结构。上部可以是拱形箱梁或拱形桁架,在一端固定,一端允许水平滑移来建立预应力,即“成形状态”,上弦受弯曲应力,成形后在“荷载状态”为轴心受压承受压应力,上部截面由压应力控制。

弹性模量为定值,则张弦桁架的刚度与上、下部截面和张弦桁架高度平方成正比,因此选择结构的高跨比f1/L和垂跨比f2/L十分重要。
拟化后的上部拱形桁架可近似看作为多跨连续粱,张弦桁架的撑杆作为此连续粱的支点。因此视索预应力值和基本风压值的大小,上部拱形桁架的上弦承受压力、下弦承受压力(或较小的拉力)、腹杆的内力表现为拉压交替变化的特征,上、下弦以应力差承担结构的抗弯作用,腹杆以拉压应力承担结构的抗剪作用。
二.北京农展馆张弦桁架设计
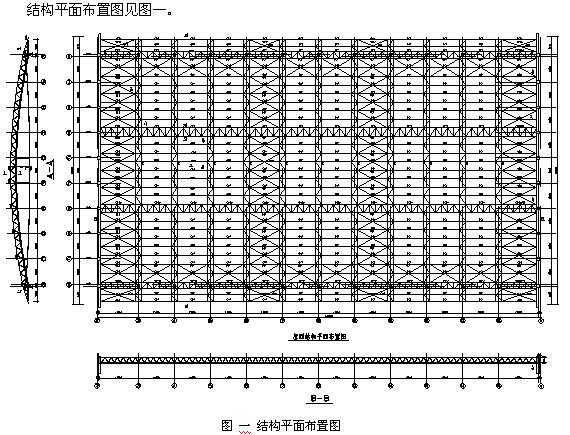
北京农展馆新馆是2004年为适应发展需要而新建的展览馆,新馆长150m(柱距12m),宽86m,建筑面积约15000m2,建筑高度(檐口)约10米。屋盖为张弦桁架结构,跨度为76m。下部为钢筋砼框架、独立基础。建筑结构的安全等级为二级,使用年限为50年。重要性系数为1.0。
张弦桁架上部设计为倒三角形拱形桁架,其高度取跨度的1/30即2.5M,单元分割按径向等分,弧长约为3M,约每隔8M设一道撑杆,缆索采用《斜拉桥热挤聚乙稀高强钢丝拉索技术条件》(GB/T18365-2001)标准。
结构沿柱距方向布置张弦桁架,沿纵向设置檩条和支撑。张弦钢桁架的面外稳定决定于结构的屋面刚度(加设过多的纵向联系构件会破坏建筑的美感),因此结构纵向支撑的布置和檩条的选用十分关键。设计时尽量将檩条加密,选用截面性能较好的矩形钢管作为檩条(兼作纵向撑杆),沿纵向设四道通长的三角形空间桁架,使其对张弦桁架提供有效的约束,形成较大的纵向空间刚度 ,求得纵横两向刚度的均匀。建筑物两端山墙设钢筋砼抗风框架,避免了山墙处张弦桁架与下部结构的复杂连接。
由于屋盖钢结构附加在钢筋砼框架结构屋顶,自重较轻,对风的作用非常敏感,设计结构的刚度充分考虑风振的影响,使结构在各种可能的荷载作用下,均具有有效恒定的刚度,并应使其固有频率偏离北京本地风的频率,避免结构发生共振效应。
1.缆索预拉力的确定原则
张弦钢桁架结构作为一种预应力钢结构体系,结构中所施加的缆索预拉力是整个结构
刚度的重要来源,因此,确定这种结构体系的预拉力值非常重要。
缆索预拉力值的确定必须通过结构的整体有限元分析来完成,并应使结构在各种可能
的荷载工况作用下处于良好的受力状态,具有良好的动力特性。
预拉力值的大小不仅决定结构的受力状态,而且决定结构整体的刚度和动力特性。
定义预应力索的三种状态:1)零状态,索施加预应力前的索段施工放样状态,即结构成形的起始状态;2)初始状态,结构在自重和预应力作用下的平衡状态,为结构承载变形的起始状态;3)荷载状态,即结构在承载后的平衡状态。
一般情况下确定索的形状问题分为三类:初始几何参量为已知量,预应力分布为未知量;初始几何参量为未知量,预应力分布为已知量;初始几何参量和预应力分布均为未知量。
本工程索的几何形状,即高跨比和垂度建筑已经有了明确的要求,接下来只是确定索的预应力分布问题了。
由上分析我们可以看出索的初始预拉力不是一个恒定的值,它同结构的几何形态、拱形桁架的刚度、荷载状况和吊装条件相关,结构设计阶段索预拉力值确定的原则是:1)在初始状态下(张弦桁架吊装状态),施加预拉力必须保证结构不能有大的变形、杆件不能失稳和破坏;2).在荷载状态下缆索不失效,在地震反应下不退出工作。索的实际预应力一般控制在0.35P~0.4P之间,以防止锚固端松弛不利现象发生。
2.缆索初始预拉力的确定
首先用逆迭代法找出结构在自重作用下不发生变形(设计几何尺寸)时索的初始预拉力值。由于索的长度较小,分析时不考虑其非线性。分析软件采用MIDAS-gen。
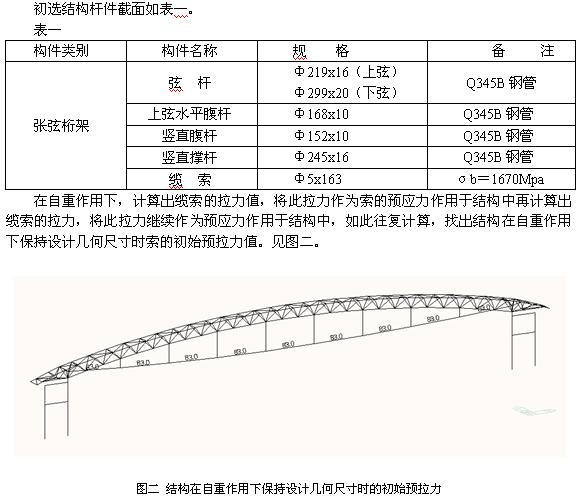
张弦桁架左端设为固定铰,右端水平约束释放,得出初始预拉力值为830KN。以此为基础逐渐加大初始预拉力值,施加设计荷载(荷载组合)计算出结构的内力和变形,再进行调整,如此往复。
1) 基本计算数据
基本风压 0.45kN/m2
风压高度变化系数为1.4,风振系数为1.162,体形系数为-0.8
基本雪压 0.40kN/m2
建筑所在地区的抗震设防烈度为 8度
设计基本地震加速度值为0.20g
设计地震分组为第一组
场地土类别为III类
2) 屋面荷载
恒载标准值 0.50 kN/m2(其中悬挂荷载 0.30 kN/m2)
主体结构及檩条自重由计算程序自动计入
3)荷载组合
考虑荷载组合对结构的不利影响,将缆索预拉力作为恒载,取以下基本荷载组合。实际计算时,考虑到结构只有在结构初始刚度相同时才能满足以下组合,故将荷载效应组合转化为荷载工况:
组合工况一:1.2x恒载+1.4x活载
(1.2DL+1.4LL)
组合工况二:1.0x恒载+1.0x活载
(1.0DL+1.0LL)
组合工况三:1.2x恒载+1/2跨x1.4x活载
(1.2DL+0.7LL)
组合工况四:1.0x恒载+1/2跨x1.0x活载
(1.0DL+0.5LL)
组合工况五:1.2x恒载+1.4x风载
(1.2DL+1.4WL)
组合工况六:1.0x恒载+1.4x风载
(1.0DL+1.4WL)
组合工况七:1.2x恒载+1.4x活载+1.4x0.6x风载
(1.2DL+1.4LL+0.84WL)
组合工况八:1.2x恒载+1.4x1.0x风载+1.4x0.7x活载+1.3x0.2x地震荷载
(1.2DL+1.4WL+0.98LL+0.26Ex)
(1.2DL+1.4WL+0.98LL+0.26Ey)
组合工况九:1.2x恒载+1.4x0.5x活载+1.3x地震荷载
(1.2DL+0.7LL+1.3Ex)
(1.2DL+0.7LL+1.3Ey)
活荷载和雪荷载取大值计算,水平地震荷载和风荷载组合时考虑与侧向水平风荷载同向组合。
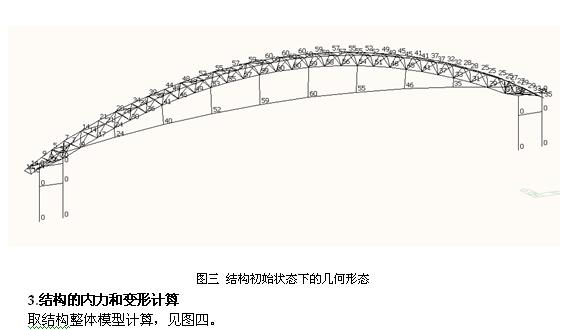
最终得出索初始预拉力值为1350KN。在自重和索初始预拉力1350KN作用下,计算出张弦桁架初始状态下的几何形状,如图三所示。最大变形量Z向为60MM,X向(滑动支座)为-30MM。此时下部索承受的实际拉力为870KN。
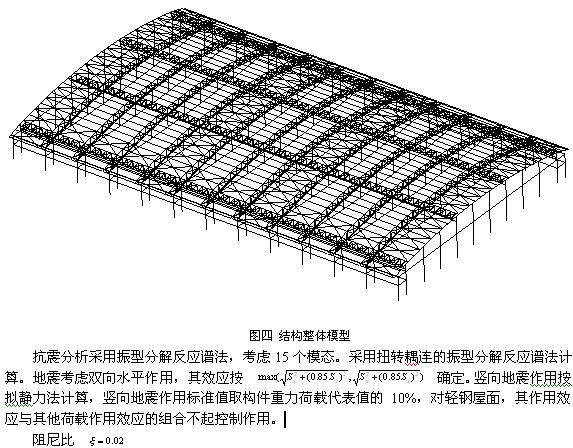
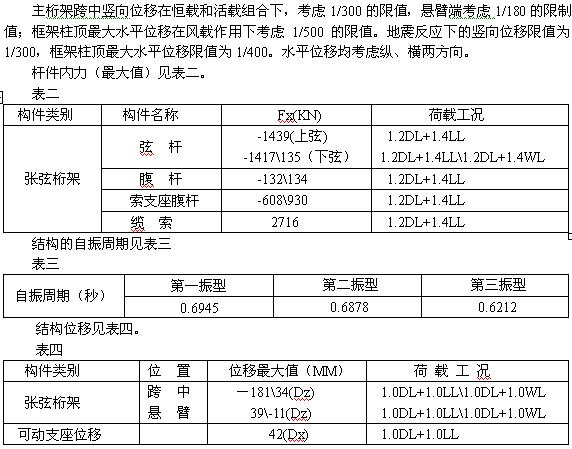


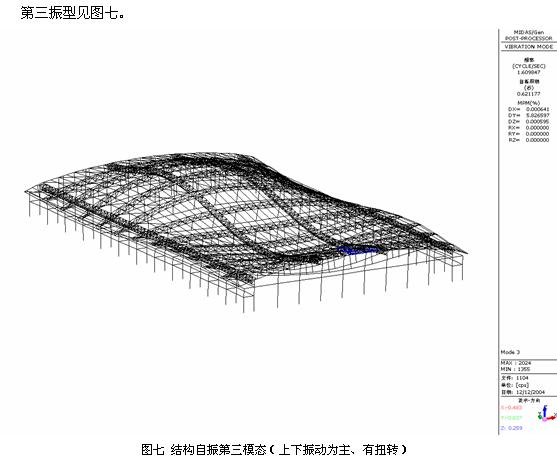
通过以上计算分析,我们可以看到,由于采用了合理的结构设计方案,结构保持了很好的整体稳定性。结构自振主振型为上、下垂直振动,避免了张弦桁架下部索面外的摆动。
三.结论
张弦桁架结构作为一种自平衡体系,它发挥了钢索抗拉强度高和拱形桁架抗压(拉)性能良好的特点,结构受力合理,能够达到很大的跨度。如广东国际会展中心、哈尔滨国际会展中心等均采用此种结构。通过北京农展馆项目设计分析,得出如下几点体会:
1.张弦桁架结构虽然作为一种自平衡体系,对下部结构没有水平推力,但作计算分析时应取包含下部结构的整体模型。通过对整体模型和张弦桁架单独计算(支座仍按不动铰和水平可动铰)的分析比较,两者的竖向变形差异达到30%,在工程设计中不容忽略。下部结构刚度越小,差异越大。两者的差异还表现在下部结构的地震反应上,下部结构单独计算(将上部张弦桁架视为荷载)和结构整体分析,地震反应亦有较大的差异。
2.张弦桁架结构一般跨度较大,屋面自重轻,在基本风压较大的地区,风的吸力有可能将导致下部钢索拉力丧失,结构失稳。设计时要尤为注意,必要时需加大结构的自重。
3.为保证竖直撑杆与上部拱形桁架和下部索为理想铰接,上部采用轴承式铰,下部采用索球铰。考虑到撑杆在张弦桁架面外必须具有刚度,因此上部轴承式铰仅为面内铰,面外须有一定的刚度。
4.用输入索预拉力作为预应力的方法分析计算时,荷载效应组合必须转换为荷载组合工况。否则索预拉力会被重复计入,得到不真实的结果。
5.确定索的初始预拉力时,既要考虑到结构荷载状态下张弦桁架的安全,又要考虑到结构初始状态的下的稳定,两者缺一不可。
参 考 文 献
1. 钟善桐.预应力钢结构.哈尔滨工业出版社,1986.
2. 陈绍蕃.钢结构设计原理.科学出版社.1987,1998(第二板).
3. 汪大绥,张富林等.上海浦东国际机场(一期工程)航站楼钢结构工程与设计.建筑结构学报,1999.
4. 陆广毅等.广州国际会展中心展览大厅钢屋盖设计.空间结构,2002,3.
5. 陆赐麟等.现代预应力钢结构.人民交通出版社.2003.