1.前言
在以杆元作为基本分析单元的结构中,构件的基本设计内力除了设计中通常考虑的轴力、弯矩和剪力外,还有绕杆轴的扭转作用。在现有的钢结构设计规范中已经给出了轴力、弯矩和剪力的验算公式,并已经在市场上通用的设计软件中加以应用。但对于扭转作用的验算,则大多是通过一些经验性的方式进行处理的,比如在管桁架结构的分析设计中认为组成管单元的闭口管构件有较好的抗扭能力而且构件中计算得到的扭转作用相对较小可以忽略,又如在网架结构中通过节点的设计可以将扭矩释放。但在某一些特定的承载情况中,构件中的扭转作用不仅数值较大,其产生的应力与轴力、弯矩、剪力产生的应力相比不可忽略,这时就要对于构件进行扭转分析验算,必要时要通过构造的措施对扭转作用予以转化分担。
本文中笔者就在工作中遇到的需要作扭转分析的特定情况作详细的介绍。
2.钢结构构件扭转性能分析
钢结构构件(特别是轻钢结构的构件)一般满足以下的尺寸比例:
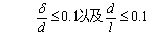
(式中δ是构件的板件厚度,d是构件的截面尺寸,l是构件的长度)
符合开口薄壁杆件的几何特征。构件除了在自由扭转时剪切应力沿厚度方向线性分布外,还具有以下的扭转特性:
1)不仅扭转时截面将发生翘曲,拉伸和弯曲时也有可能发生翘曲(如当弯矩作用平面未通过构件的弯心时,构件会发生双弯曲现象)。
2)翘曲受到约束,扭转时不仅会产生切应力还将产生正应力,这一正应力与拉伸和弯曲产生的正应力相比不可忽略;拉伸和弯曲时也会产生正应力,继而还会产生附加的切应力。
与一般的结构构件不同,开口薄壁杆件的计算尚要计算截面的扇性几何性质,这是计算其截面约束扭转的基础。将杆件截面按壁厚中线简化成线元后,对于某个极点可以计算出线元各点的扇性面积坐标Aω,并进一步计算出截面的其他扇性几何性质Sω(扇性静矩),Iω(扇性惯性矩),IωY(对y轴的扇性惯性积),IωZ(对z
轴的扇性惯性积)

图中s-中线弧长;ds-弧长微段;O-弧长起点(零点);P-极点。
选择合适的零点,可以使主扇性静矩等于零,这时的零点称为“主扇性零点”,对应的扇性面积Aω称为“主扇性面积”。
选择合适的极点,可以使扇性惯性积等于零,这时的极点称为“主扇性极点”,对应的扇性惯性矩Iω称为“主扇性惯性矩”。 主扇性极点就是构件的弯曲中心。
构件受扭时,与构件长度方向垂直的截面绕某一不动点转动,这一不动点称为“扭转中心”,截面绕扭转中心转动,各点会产生沿构件长度方向的纵向位移;开口构件各点纵向位移不等,这样便产生翘曲,这种位移被称为“翘曲位移”。
当构件是自由扭转时(即开口薄壁杆件各截面上所承受的扭矩均相等,而且支承条件不限制端面的翘曲,则扭转角j沿杆件长度方向的变化率q保持不变,各截面产生相同的翘曲位移,而且是自由的)不产生纵向的正应力,而仅有剪切应力,扭转角j及其变化率q和剪切应力τK可由下列公式计算
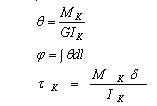
(以上式中MK是杆件截面上的纯扭矩,G是杆件材料的剪切模量,IK是截面的抗扭惯性矩)
而当若杆件上沿轴线方向作用有分布不均匀的扭矩,或支承处的约束限制了截面的自由翘曲,这时的扭转称为“约束扭转”。由于沿构件长度方向的纵向翘曲位移受到约束,构件内存在附加的翘曲正应力σω,对于构件整体来说,即存在弯曲扭转双力矩B和弯曲扭转力矩Mω:
在建筑结构设计手册中,可以查到典型的支承条件和荷载条件下弯曲扭转双力矩B和弯曲扭转力矩Mω的计算公式,根据以上的公式就可以得到构件内约束扭转的翘曲正应力以及剪应力。

3.含有扭转应力项的钢结构构件的验算式
现行钢结构设计规范没有规定当在结构构件中含有扭转应力项时应如何进行设计校验,但参考现行的薄壁型钢设计规范,采用以下的强度验算式和稳定验算式:
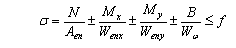
4.在工程中遇到的需要验算作用的情况实例:带有转臂吊的厂房柱
笔者经历的一项轻钢建筑工程,该车间是单跨带吊车的钢结构建筑物,柱子中心间距25.95米;柱顶标高11.65米;安装有两台轨顶标高8.9米,轨距25米,起重量20吨的空中操作中级工程制吊车;吊车梁跨度6米;在局部因工艺需要抽除一根边柱,为此设计了跨度12米的吊车梁和相应的屋面托梁;建筑物的一面侧墙的柱子需要考虑在二期扩建时承担两台同样起重量的吊车及相应的屋面荷载。
从建筑规模、设计荷载考虑都是很普通的案例,唯一较为特殊的特征建筑的每一根柱子上都要能安装起重量1.6吨,最大回旋半径5米,转臂标高5米的转臂吊。在竣工验收阶段使用方反映试吊时当转臂转到偏离钢架平面接近90度时,点动加载,柱子扭转、吊臂端部明显下沉,使用方对此表示了强烈不安。由于设计阶段已经考虑到了转臂吊荷载情况,并采取了构造措施,实际变形偏离原始设计意图,笔者进行了实地考察并进行了如下分析。
本项目钢构设计按平面框排架结构建模设计,转臂吊在框架平面内起吊对钢架计算附加的弯矩(M=127KNm设计值)作为可变荷载考虑。但当转臂转动到与钢架平面垂直的方向上时,由于转臂吊连接在钢柱的一侧翼缘上,转臂吊的附加弯矩作用平面不通过钢柱的弯曲中心,除了对于钢柱弱轴平面内的弯矩作用外,还有扭转双力矩作用,计算表明含有这一双力矩作用的内力组合对于钢柱的内力是起控制作用的。
钢柱采用H800X350X8X14的焊接H型钢,为了保证转臂吊转臂转到垂直与钢架平面的方向时构件的承载性能,在连接转臂吊一侧的翼缘上连接了C400X100X10X10的焊接槽钢作为加强。
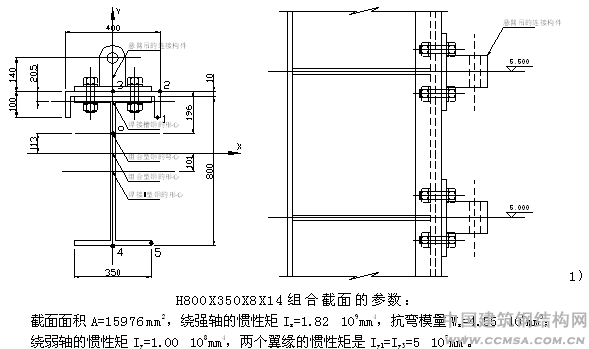
焊接槽钢C400X100X10X10的截面参数:
截面面积A=5800mm2,形心距槽钢腹板的边缘是20.52毫米;
绕平行于槽钢腹板的主轴的惯性矩Ix’=2.82 106mm4;
绕垂直于槽钢腹板的主轴的惯性矩Iy’=1.22 108mm4。
焊接H型钢与焊接槽钢的组合截面的截面参数:
形心与焊接H型钢的形心的距离是a=101.08mm;
截面弯心与焊接槽钢的腹板距离是b=195.97mm;
组合截面的惯性矩Ix=1.82 109+159761012+2.82106+5800(309-20.52)2=2.468109mm4
Iy=1.22 108+1.00108=2.22108mm4
组合截面中各点的抗弯模量分别是:
①点Wx=1.181 107mm3,②、③点Wx=7.989 106mm3,④、⑤点Wx=4.927 106mm3;
①、②点Wy=1.11 106mm3,③、④点Wy=0,⑤点Wy=1.27 106mm3。
组合截面中相对于“O”点的各点的扇性面积坐标是:
①点Aω=18525mm2,②点Aω=36075mm2,③、④点Aω=0mm2,、⑤点Aω=106225mm2。
组合截面中相对于“O”点的各点的扇性面积矩是:
①、⑤点Sω=0mm4,②点Sω=2.43 107mm4,③点Sω=10.17 107mm4,④点Sω=10.17 107mm4。
组合截面的扇性面积矩Iω由积分得到Iw=2.35 1013mm6
截面的抗扭惯性矩Ik=1.25 106mm4
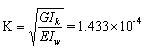
在计算出上述的几何参数后,可以根据结构设计手册,查一端嵌固的转臂梁在偏离弯心平面的弯矩作用下的内力公式计算结构中的弯扭双力矩和扭矩。
弯矩作用于距焊接槽钢外侧140毫米处,距离构件形心的距离是e=449mm,作用点的标高L=5000mm,KL=0.716,则计算参数:
sh(kl)=0.779,ch(kl)=1.268,th(kl)=0.615;
当柱上作用有一台转臂吊后附加的双力矩是:

主体结构的钢材均为Q345,由计算表明,上述应力水平是在安全范围之内的。
实地考察时,发现在转臂吊起吊时,钢柱的截面不仅存在整体的扭转现象,连接了焊接槽钢的一侧翼缘尚有局部翘曲情况,实地观察后发现在厂房结构完成安装后,使用方出于安装机电设备的考虑拆除了在连接转臂吊节点处钢柱的两对横向加劲肋,笔者对于这一情况的判断是由于拆除加劲肋,仅靠8毫米厚的腹板不足以保证截面的平面几何不变。连接到一侧翼缘的转臂吊节点的作用力不能被整个截面均匀承担,柱子局部板件在集中荷载的作用下发生了翘曲。
而要考察局部翘曲的变形状态,笔者采用壳单元对柱段进行有限元分析,对柱子承受平面外偏心弯矩下节点的变形进行了计算。目的是计算出柱子各个标高截面的扭转角度,并确定这一的扭转对于转臂吊端点位移的影响程度。在柱子截面的切除加劲肋后柱子翼缘是否能安全承载?
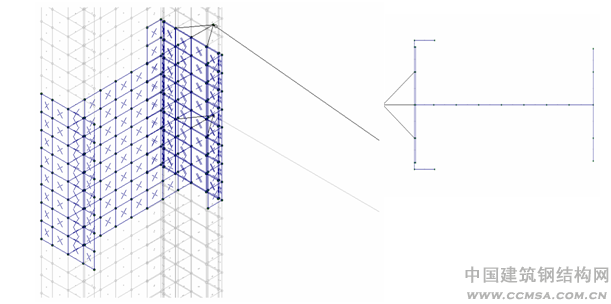
上图显示了有限元模型的局部和剖面示意,这一模型将柱子的截面简化成壳单元,单元厚度与相应板件的厚度一致,为了模拟焊接槽钢与焊接H型钢的连接焊缝,在两者之间设置了厚度相当于6毫米角焊缝的连接单元。图中由节点引出模拟转臂吊吊轨和拉杆的杆件单元,1.6吨的吊重就作用在吊轨端部。计算表明,当按设计意图在相应的节点设置加劲肋后,截面基本保持原来的形状,截面变形是组合型钢形心的平动和绕形心的转动。柱子上标高5米和5.5米转臂吊连接点处在弯矩作用平面内有±1.3毫米的水平位移(x向),这一变形相当于转臂吊的支座存在2.6/500=1/192的角变形,转臂5米的下沉量是26毫米。柱子板件内由于弯曲扭转产生的最大弯曲应力是95N/mm2,这一结果与采用结构力学公式的结果是相当的。
但在去除了加劲肋后的模型中。截面受力后不再保持原来的形状,截面变形分成两部分,一部分远离转臂吊连接节点(图中O-5的部分)转动较小,而与节点相连的(1-O部分)则表现出很大的转动,显示出腹板没有足够的刚度保证截面的几何不变。在转臂吊作用下,柱子上标高5米和5.5米的转臂吊连接点处在弯矩作用平面内有±3.5毫米的水平位移,而最大的翼缘翘曲达到了±5.1毫米,这一变形相当于转臂吊的支座存在7/500=1/70的角变形,转臂5米即有70毫米的下沉量,加上点动加载的冲击作用,转臂吊难以使用。计算还表明柱子板件内由于弯曲扭转加上板件的局部翘曲产生的最大弯曲应力达到了365N/mm2,超过了材料的屈服强度,考虑到这一应力还要叠加结构平面内计算所得到的内应力,所以去除加劲肋在影响转臂吊使用的同时,对结构整体的安全也产生了威胁。在这样的分析基础上笔者要求业方恢复被切除的加劲肋,经反复说明转臂吊的下沉是由于钢柱的加劲肋去除后板件局部翘曲引起的,采用其他方法均不如恢复加劲肋有效,业方最终接受了这一解决方案。
5.结束语
以上是在对一个实际工程案例,结合设计计算手册的公式和有限元电算对于钢柱受弯扭作用下变形、应力的分析过程。从中可以看到,考虑了扭转作用后,即使结构内应力仍小于材料的屈服极限,由于开口薄壁构件的抗扭刚度较小,构件也会因为过大的扭转变形而导致使用功能的丧失,需要设计工程师根据结构构件的特点采用有限元电算手段进行进一步的分析。特别在集中荷载作用位置处,缺少抗扭构造措施,还会引起板件的局部翘曲现象,影响到结构的安全,这一点在设计和施工中要注意避免。
参考书目:
中国建筑工业出版社《建筑结构静力计算手册》
转载自中国建筑金属结构协会建筑钢结构网(www.CCMSA.com.cn)